Using optweight to Estimate Stable Balancing Weights

Introduction

optweight implements stable balancing weighting (SBW) as described by Zubizarreta (2015). This involves estimating weights aimed at adjusting for confounding by balancing covariates while minimizing some measure of variability of the weights. SBW is also known as empirical balancing calibration weighting (Chan, Yam, and Zhang 2016) and entropy balancing (Källberg and Waernbaum 2023). These methods are related to inverse probability weighting (IPW), and there are some equivalences between SBW and IPW (Y. Wang and Zubizarreta 2020). While IPW typically involves fitting a propensity score model for the probability of receiving treatment, SBW estimates weights directly that balance the covariates. The distinction between these two approaches is described in detail by Chattopadhyay, Hase, and Zubizarreta (2020).

SBW involves solving the following optimization problem:

\[\begin{align} \min_{\mathbf{w}} \quad & f(\mathbf{w}, \mathbf{b},\mathbf{s}) \\ \text{s.t.} \quad & \sum_{i:A_i=a} {s_i w_i} = \sum_{i:A_i=a} {s_i b_i} \quad \forall a \in \mathcal{A} \\ & \left| \frac{\sum_{i:A_i=a} {s_i w_i x_{k,i}}}{\sum_{i:A_i=a} {s_i w_i}} - \bar{x}_k^* \right| \le \delta_k \quad \forall a \in \mathcal{A}, \forall k \in \{1, \dots, K\} \\ & w_i \ge \varepsilon \quad \forall i \end{align}\]

where \(\mathbf{w}=\{w_1, \dots, w_N\}\) are the estimated weights, \(\mathbf{s}=\{s_1, \dots, s_N\}\) are sampling weights, \(\mathbf{b}=\{b_1, \dots, b_N\}\) are “base” weights, \(A_i\) is a categorical treatment taking on values \(a \in \mathcal{A}\), and \(x_{k,i}\) is the value of covariate \(\mathbf{x}_k\) for unit \(i\). \(f(\mathbf{w}, \mathbf{b},\mathbf{s})\) is the objective function to minimize, a function of the estimated weights, base weights, and sampling weights. \(\delta_k\) is the balance tolerance for covariate \(k\), \(\bar{x}_k^*\) is the target value for covariate \(k\), and \(\varepsilon\) is the minimum weight allowed.

Generally, \(f\) represents a measure of dispersion from the base weights, weighted by the sampling weights. The original formulation of SBW used \(f(\mathbf{w}, \mathbf{b},\mathbf{s}) = \frac{1}{N}\sum_i{s_i(w_i-b_i)^2}\), the weighted L2 norm. Entropy balancing uses \(f(\mathbf{w}, \mathbf{b},\mathbf{s}) = \frac{1}{N}\sum_i{s_i w_i \log\left(\frac{w_i}{b_i}\right)}\), the weighted relative entropy between the estimated and base weights.

The interpretation of these constraints is as follows:

The first constraint is a scaling constraint that establishes a meaningful scale for the weights \(\mathbf{w}\). In particular, that scale is determined by the base weights \(\mathbf{b}\).
The second constraint is the balance constraint. A target value \(\bar{x}_k^*\) can be chosen for each covariate, and the weighted mean of the covariates in each treatment group must be within some tolerance \(\delta_k\) of that target. That also guarantees the weighted means between treatment groups are within some tolerance of each other. It is possible to forgo a specific target and just require the weighted means to be equal to each other.
The final constraint is optional and restricts the minimum value of the weights. For some \(f\), the weights can be unbounded, and it is up to the user to require the weights to fall within some range. The original formulation of SBW used \(\varepsilon = 0\), but omitting this constraint altogether, which allows the weights to be negative, is also possible.

Asymptotic properties of SBW are described in Y. Wang and Zubizarreta (2020). In general, the weights are precise and perform well, and adding approximate balance constraints (i.e., using \(\delta_k>0\)) tends to improve precision without greatly affecting bias. There is also a weak double-robustness property to the weights: the estimate is consistent if either the outcome model corresponds to the balance constraints or the implicit propensity score model corresponds to the true propensity score model. Different forms of \(f\) imply different assumptions about the propensity score model. Allowing \(\varepsilon\) to be negative allows for the possibility of negative weights, which can improve precision but induce extrapolation. It turns out that using a linear regression model for the outcome is equivalent to using SBW with the L2 norm, \(\delta_k=0\), and \(\varepsilon=-\infty\) (Chattopadhyay and Zubizarreta 2023).

Often \(\bar{x}_k^*\) are chosen to represent a known target group, like the full sample when targeting the ATE or the treated group when targeting the ATT. They can also be chosen to generalize the effect estimate to an arbitrary target population (Chattopadhyay, Cohn, and Zubizarreta 2024).

SBWs can be generalized to continuous treatments, in which case instead of balancing the covariate means, the treatment-covariate covariances are constrained to be balanced. This was explored in Greifer (2020), Tübbicke (2022), and Vegetabile et al. (2021). SBW can also be used to directly weight a sample to resemble a population, without needing to balance two treatment groups. This also known known as matching-adjusted indirect comparison [MAIC; Phillippo et al. (2020), Signorovitch et al. (2010)].

optweight contains functionality to perform these operations and assess their performance. It was designed to be user-friendly, compatible with the syntax used with WeightIt, and supported by cobalt for balance assessment, at the possible expense of some flexibility. The sbw package also implements some of these methods, prioritizing different aspects of the estimation. Entropy balancing is implemented in WeightIt, which also calls optweight to provide a simpler interface to SBW.

Using optweight

The main function in optweight is optweight(), which uses a formula interface to specify the treatment, covariates, and balance tolerance. Other functions in optweight simplify specification of more detailed parameters and support diagnostics.

Below, we’ll use optweight() to estimate weights that balance the covariates in an observational study. We’ll use the lalonde dataset in cobalt and target the ATT first. The treatment is treat, the outcome is re78, and the other variables are the covariates to balance.

library(optweight)

data("lalonde", package = "cobalt")

head(lalonde)

##   treat age educ   race married nodegree re74 re75    re78
## 1     1  37   11  black       1        1    0    0  9930.0
## 2     1  22    9 hispan       0        1    0    0  3595.9
## 3     1  30   12  black       0        0    0    0 24909.5
## 4     1  27   11  black       0        1    0    0  7506.1
## 5     1  33    8  black       0        1    0    0   289.8
## 6     1  22    9  black       0        1    0    0  4056.5

optweight() can be used simply by supplying the treatment can covariates to the formula argument, the dataset to the data argument, and the estimand to the estimand argument (here, the ATT). By default, optweight() minimizes the L2 norm, requires exact mean balance on the covariates, and requires all weights to be greater than \(10^{-8}\).

ow <- optweight(treat ~ age + educ + race + married + nodegree +
                  re74 + re75, data = lalonde,
                estimand = "ATT")
ow

## An optweight object
##  - number of obs.: 614
##  - norm minimized: "l2"
##  - sampling weights: present
##  - base weights: present
##  - treatment: 2-category
##  - estimand: ATT (focal: 1)
##  - covariates: age, educ, race, married, nodegree, re74, re75

Using cobalt::bal.tab() on the output computes the weighted balance statistics.

cobalt::bal.tab(ow)

## Balance Measures
##                Type Diff.Adj
## age         Contin.       -0
## educ        Contin.       -0
## race_black   Binary       -0
## race_hispan  Binary        0
## race_white   Binary        0
## married      Binary       -0
## nodegree     Binary       -0
## re74        Contin.       -0
## re75        Contin.       -0
## 
## Effective sample sizes
##            Control Treated
## Unadjusted   429.      185
## Adjusted     108.6     185

As expected, all mean differences are exactly 0 in the weighted sample. We can use summary() to examine some properties of the weights:

summary(ow)

##                   Summary of weights
## 
## - Weight ranges:
## 
##         Min                                 Max
## treated   1      ||                       1.   
## control   0 |---------------------------| 6.002
## 
## - Units with the 5 most extreme weights by group:
##                                      
##              1     2    3     4     5
##  treated     1     1    1     1     1
##            423   388  226   196   118
##  control 5.568 5.602 5.67 5.922 6.002
## 
## 
## - Weight statistics:
## 
##            L2    L1    L∞ Rel Ent # Zeros
## treated 0.    0.    0.       0.         0
## control 1.717 1.339 5.002    1.23       0
## 
## - Effective Sample Sizes:
## 
##            Control Treated
## Unweighted   429.      185
## Weighted     108.6     185

summary() produces some information about the distribution of weights, including different measures of the dispersion of the weights, each of which corresponds to one of the allowed objective functions to minimize. L2 is the square root of the mean squared deviation of the estimated weights from the base weights (i.e., the L2 divergence); here, the base weights are all 1. See ?summary.optweight for more information about the other statistics. Lastly, summary() produces the weighted and original (effective) samples sizes.

We can use plot() on the summary() output to visualize the distribution of the weights:

summary(ow) |> plot()

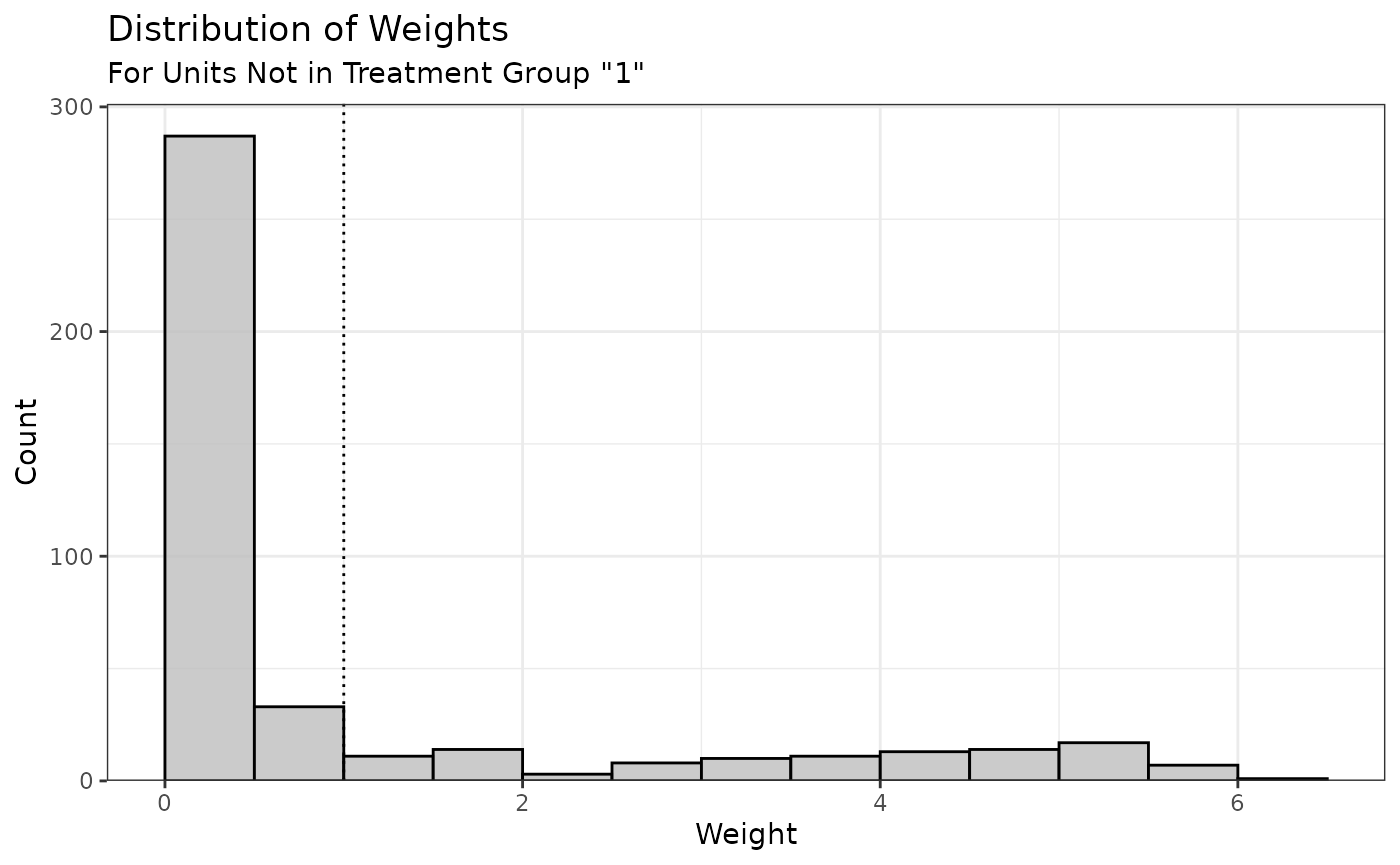
Because we targeted the ATT, only the weights for the control group are displayed (the treated group weights are all 1).

Below, we’ll adjust a few arguments to see what affects they have on the weights.

`tols`

The balance tolerance is controlled by the tols argument. This can either be a single value applied to all variables or a vector with a value for each covariate. By default, tols = 0. Let’s see what happens when we increase tols to .02.

ow2 <- optweight(treat ~ age + educ + race + married + nodegree +
                   re74 + re75, data = lalonde,
                 estimand = "ATT",
                 tols = .02)

cobalt::bal.tab(ow2)

## Balance Measures
##                Type Diff.Adj
## age         Contin.     0.02
## educ        Contin.     0.02
## race_black   Binary     0.02
## race_hispan  Binary     0.00
## race_white   Binary    -0.02
## married      Binary    -0.02
## nodegree     Binary     0.02
## re74        Contin.    -0.02
## re75        Contin.     0.02
## 
## Effective sample sizes
##            Control Treated
## Unadjusted   429.      185
## Adjusted     118.8     185

Now, all mean differences are less than .02. Note that by default, cobalt::bal.tab() reports standardized mean differences for continuous variables and raw mean differences for binary variables. optweight() standardizes the balance tolerances the same way: by default, tols refers to the largest standardized mean difference allowed for continuous variables and the largest raw mean difference for binary variables. To change whether tolerances for binary or continuous variables should be in standardized units or not, see the std.binary and std.cont arguments of optweight.fit(), which optweight() calls under the hood.

Allowing for more relaxed imbalance also increases the ESS. The L2 statistic has shrunk correspondingly:

summary(ow2, weight.range = FALSE)

##                   Summary of weights
## 
## 
## - Weight statistics:
## 
##            L2    L1    L∞ Rel Ent # Zeros
## treated 0.    0.    0.      0.          0
## control 1.616 1.267 4.212   1.118       0
## 
## - Effective Sample Sizes:
## 
##            Control Treated
## Unweighted   429.      185
## Weighted     118.8     185

To supply each covariate with its own tolerance, a named vector must be supplied. This can sometimes be a little tedious, so there is a helper function, process_tols(), that simplifies this. Give process_tols() the formula and dataset (and, optionally, an initial tolerance value or vector thereof), and it will return a modifiable vector of balance tolerances that can be supplied to optweight().

tols <- process_tols(treat ~ age + educ + race + married + nodegree +
                       re74 + re75, data = lalonde,
                     tols = .02)
tols

##  - tols:
##      age     educ     race  married nodegree     re74     re75 
##     0.02     0.02     0.02     0.02     0.02     0.02     0.02

Here, we’ll relax the constraint on race and then estimate the weights.

tols["race"] <- .07

tols

##  - tols:
##      age     educ     race  married nodegree     re74     re75 
##     0.02     0.02     0.07     0.02     0.02     0.02     0.02

ow3 <- optweight(treat ~ age + educ + race + married + nodegree +
                   re74 + re75, data = lalonde,
                 estimand = "ATT",
                 tols = tols)

cobalt::bal.tab(ow3)

## Balance Measures
##                Type Diff.Adj
## age         Contin.     0.02
## educ        Contin.     0.02
## race_black   Binary     0.07
## race_hispan  Binary     0.00
## race_white   Binary    -0.07
## married      Binary    -0.02
## nodegree     Binary     0.02
## re74        Contin.    -0.02
## re75        Contin.     0.02
## 
## Effective sample sizes
##            Control Treated
## Unadjusted   429.      185
## Adjusted     132.7     185

We can see that for all covariates other than race, the mean differences are at or below .02, but for race, the mean differences are at or below .07. This led to an increase in ESS due to the relaxed constraints.

`norm`

The norm argument controls which objective function is used. The allowable arguments are "l2" for the L2 norm (the default), "l1" for the L1 norm, "linf" for the L\(\infty\) norm, "entropy" for the relative entropy, and "log" for the sum of the negative logs. The most thorough theoretical work has been done on the L2 norm and relative entropy, and these tend to be the easiest to optimize.

Weighting by minimizing the relative entropy is also known as “entropy balancing” (Hainmueller 2012; Källberg and Waernbaum 2023; Zhao and Percival 2017) and is available in WeightIt, which uses a more parsimonious representation of the problem. Weighting by minimizing the sum of negative logs is equivalent to nonparametric covariate balancing propensity score (npCBPS) weighting (Fong, Hazlett, and Imai 2018), which maximizes the empirical likelihood of the data to estimate the weights. A penalized version of npCBPS is available in CBPS and in WeightIt (which calls functions from CBPS), but optweight offers additional options not possible in those packages, such as specifying balance tolerances, targets, and different estimands.

Different solvers are available for each norm; see ?optweight.fit() for details.

Below, we’ll minimize the L2 norm, L1 norm, L\(\infty\) norm, and relative entropy and see how those choices affect the properties of the weights.

# L2 norm
ow_l2 <- optweight(treat ~ age + educ + race + married + nodegree +
                     re74 + re75, data = lalonde,
                   estimand = "ATT",
                   norm = "l2")

summary(ow_l2, weight.range = FALSE)

##                   Summary of weights
## 
## 
## - Weight statistics:
## 
##            L2    L1    L∞ Rel Ent # Zeros
## treated 0.    0.    0.       0.         0
## control 1.717 1.339 5.002    1.23       0
## 
## - Effective Sample Sizes:
## 
##            Control Treated
## Unweighted   429.      185
## Weighted     108.6     185

# L1 norm
ow_l1 <- optweight(treat ~ age + educ + race + married + nodegree +
                     re74 + re75, data = lalonde,
                   estimand = "ATT",
                   norm = "l1")

summary(ow_l1, weight.range = FALSE)

##                   Summary of weights
## 
## 
## - Weight statistics:
## 
##            L2    L1    L∞ Rel Ent # Zeros
## treated 0.    0.     0.     0.          0
## control 2.082 1.281 10.83   1.239       0
## 
## - Effective Sample Sizes:
## 
##            Control Treated
## Unweighted  429.       185
## Weighted     80.42     185

# L-infinity norm
ow_linf <- optweight(treat ~ age + educ + race + married + nodegree +
                     re74 + re75, data = lalonde,
                   estimand = "ATT",
                   norm = "linf",
                   eps = 1e-5) # to improve convergence

summary(ow_linf, weight.range = FALSE)

##                   Summary of weights
## 
## 
## - Weight statistics:
## 
##            L2    L1    L∞ Rel Ent # Zeros
## treated 0.    0.    0.        0.        0
## control 1.877 1.548 3.577     1.5       0
## 
## - Effective Sample Sizes:
## 
##            Control Treated
## Unweighted  429.       185
## Weighted     94.83     185

# Relative entropy
ow_re <- optweight(treat ~ age + educ + race + married + nodegree +
                     re74 + re75, data = lalonde,
                   estimand = "ATT",
                   norm = "entropy")

summary(ow_re, weight.range = FALSE)

##                   Summary of weights
## 
## 
## - Weight statistics:
## 
##            L2    L1   L∞ Rel Ent # Zeros
## treated 0.    0.    0.     0.          0
## control 1.832 1.287 8.42   1.101       0
## 
## - Effective Sample Sizes:
## 
##            Control Treated
## Unweighted  429.       185
## Weighted     98.46     185

We can see that minimizing the L2 norm yields weights that have the lowest L2 divergence, minimizing the L1 norm yields weights that have the lowest L1 divergence, minimizing the L\(\infty\) norm yields weights that have the lowest L\(\infty\) divergence, and minimizing the relative entropy yields weights that have the lowest relative entropy. The L2 divergence has the closest correspondence to the ESS (they have a 1:1 relationship), but there are some theoretical reasons to prefer other norms, especially when they correspond to certain assumptions about the true propensity score model. See Källberg and Waernbaum (2023) for more information on these assumptions.

`estimand` and `targets`

Different estimands can be targeted by supplying an argument to estimand. Allowable estimands include the ATE, ATT, and ATC. These ensure the covariate means in each group resemble those in the full sample, the treated group, and the control group, respectively. For example, if set estimand = "ATE", both groups will be weighted so that the covariate means are equal to the covariate means in the full sample, as demonstrated below.

The covariate means in the full sample can be computed using cobalt::col_w_mean():

covs <- lalonde[-c(1, 9)]

cobalt::col_w_mean(covs)

##         age        educ  race_black race_hispan  race_white     married    nodegree        re74 
##     27.3632     10.2687      0.3958      0.1173      0.4870      0.4153      0.6303   4557.5466 
##        re75 
##   2184.9382

After estimating weights that target the ATE, we will see that the weighted covariate means in each group are equal to those in the full sample:

ow_ate <- optweight(treat ~ age + educ + race + married + nodegree +
                      re74 + re75, data = lalonde,
                    estimand = "ATE")

cobalt::col_w_mean(covs, weights = ow_ate$weights,
                   subset = lalonde$treat == 1)

##         age        educ  race_black race_hispan  race_white     married    nodegree        re74 
##     27.3632     10.2687      0.3958      0.1173      0.4870      0.4153      0.6303   4557.5466 
##        re75 
##   2184.9382

cobalt::col_w_mean(covs, weights = ow_ate$weights,
                   subset = lalonde$treat == 0)

##         age        educ  race_black race_hispan  race_white     married    nodegree        re74 
##     27.3632     10.2687      0.3958      0.1173      0.4870      0.4153      0.6303   4557.5466 
##        re75 
##   2184.9382

In addition to targeting a natural sample, it’s also possible to target a specific population by supplying an argument to targets¹. The theory behind this methodology is described by Chattopadhyay, Cohn, and Zubizarreta (2024). To request a different target population, process_targets() can be used to create a vector of target means which are supplied to the targets argument of optweight().

targets <- process_targets(~ age + educ + race + married + nodegree +
                             re74 + re75,
                           data = lalonde)

targets

##  - targets:
##         age        educ  race_black race_hispan  race_white     married    nodegree        re74 
##     27.3632     10.2687      0.3958      0.1173      0.4870      0.4153      0.6303   4557.5466 
##        re75 
##   2184.9382

By default, process_targets() computes the mean of each covariate in the full sample. These can be modified similarly to tols to specify target means. Note that for categorical covariates, the proportions in the groups must sum to 1.

targets["age"] <- 35
targets[c("race_black", "race_hispan", "race_white")] <- c(.5, .3, .2)

targets

##  - targets:
##         age        educ  race_black race_hispan  race_white     married    nodegree        re74 
##     35.0000     10.2687      0.5000      0.3000      0.2000      0.4153      0.6303   4557.5466 
##        re75 
##   2184.9382

We can supply these to optweight() to request that the covariate means in the weighted sample are equal to these target means. We need to set estimand = NULL to ensure the targets are obeyed. Failing to do this will produce a warning.

ow_target <- optweight(treat ~ age + educ + race + married + nodegree +
                         re74 + re75, data = lalonde,
                       targets = targets,
                       estimand = NULL)

# Weighted covariate means in the two groups
cobalt::col_w_mean(covs, weights = ow_target$weights,
                   subset = lalonde$treat == 1)

##         age        educ  race_black race_hispan  race_white     married    nodegree        re74 
##     35.0000     10.2687      0.5000      0.3000      0.2000      0.4153      0.6303   4557.5466 
##        re75 
##   2184.9382

cobalt::col_w_mean(covs, weights = ow_target$weights,
                   subset = lalonde$treat == 0)

##         age        educ  race_black race_hispan  race_white     married    nodegree        re74 
##     35.0000     10.2687      0.5000      0.3000      0.2000      0.4153      0.6303   4557.5466 
##        re75 
##   2184.9382

The treatment effect estimate from this method of weighting would have the interpretation of the estimate from a population with similar means to those of the sample but with a mean age of 35 years (older than the original sample) and a racial profile of 50% Black, 30% Hispanic, and 20% white.

Note that process_targets() can be supplied without a formula if targets are to be specified for all variables in data. We’ll use this syntax in the section on optweight.svy() below.

Sampling weights and base weights

Sampling weights are used when attempting to generalize the estimates from a sample to a specific target population. Some datasets come with sampling weights in order for analyses using them to be valid. These weights can be supplied to the s.weights argument of optweight(). This has three effects: 1) the balance and target constraints correspond to the product of the estimated and sampling weights, 2) the target values for the covariates are weighted by the sampling weights (if not supplied through targets), and 3) the contribution of the estimated weights to the objective function is weighted by the sampling weights. Sampling weights are also used when bootstrapping using the fractional weighted bootstrap (Xu et al. 2020), e.g., as implemented in the fwb package; see section “Estimating effects” below. By default, when s.weights is not specified, sampling weights are equal to 1.

Base weights are a set of initial weights that have some properties that the user wants to retain while enforcing balance constraints. The estimated weights are chosen to minimize their distance from the base weights, where that distance corresponds to \(f\). These weights can be supplied to the b.weights argument of optweight(). By default, when not specified, base weights are equal to 1. An example use of base weights would be to enforce balance on a set of IPW weights estimated using a flexible model that is unable to exactly balance the covariates. This strategy was used by one of the winning methods in the 2016 ACIC data competition (Dorie et al. 2019). We’ll demonstrate the use of base weights below.

First, we’ll estimate propensity score weights using generalized boosted modeling through WeightIt. This is a flexible machine learning model, and we can request that features beyond the covariate means be balanced by minimizing the largest Kolmogorov-Smirnov (KS) statistic in the weighted sample.

W_gbm <- WeightIt::weightit(treat ~ age + educ + race + married + nodegree +
                              re74 + re75, data = lalonde,
                            estimand = "ATT",
                            method = "gbm",
                            criterion = "ks.max")

Next we’ll use optweight() to estimate a set of weights that differ as little as possible (as measured by the root mean squared divergence) from these estimated weights while enforcing exact balance on the covariate means.

ow_bw <- optweight(treat ~ age + educ + race + married + nodegree +
                     re74 + re75, data = lalonde,
                   estimand = "ATT",
                   b.weights = W_gbm$weights)

We’ll also estimate SBW weights with uniform base weights to see the difference in the properties of the weights.

ow <- optweight(treat ~ age + educ + race + married + nodegree +
                  re74 + re75, data = lalonde,
                estimand = "ATT")

Finally, we can look at balance on all three sets of weights on the means and KS statistics.

# Mean diferences
cobalt::bal.tab(W_gbm, stats = "m",
                weights = list(ow_bw = ow_bw$weights,
                               ow = ow$weights))

## Balance Measures
##                 Type Diff.weightit Diff.ow_bw Diff.ow
## prop.score  Distance         0.395      0.382    1.13
## age          Contin.        -0.033      0.000   -0.00
## educ         Contin.        -0.061      0.000   -0.00
## race_black    Binary         0.013      0.000   -0.00
## race_hispan   Binary         0.006     -0.000    0.00
## race_white    Binary        -0.019     -0.000    0.00
## married       Binary        -0.022      0.000   -0.00
## nodegree      Binary         0.086      0.000   -0.00
## re74         Contin.         0.037      0.000   -0.00
## re75         Contin.         0.069      0.000   -0.00
## 
## Effective sample sizes
##          Control Treated
## All       429.       185
## weightit   32.07     185
## ow_bw      31.62     185
## ow        108.64     185

# KS statistics
cobalt::bal.tab(W_gbm, stats = "ks",
                weights = list(ow_bw = ow_bw$weights,
                               ow = ow$weights))

## Balance Measures
##                 Type KS.weightit KS.ow_bw KS.ow
## prop.score  Distance       0.189    0.183 0.488
## age          Contin.       0.086    0.118 0.283
## educ         Contin.       0.086    0.055 0.042
## race_black    Binary       0.013    0.000 0.000
## race_hispan   Binary       0.006    0.000 0.000
## race_white    Binary       0.019    0.000 0.000
## married       Binary       0.022    0.000 0.000
## nodegree      Binary       0.086    0.000 0.000
## re74         Contin.       0.045    0.041 0.226
## re75         Contin.       0.072    0.051 0.140
## 
## Effective sample sizes
##          Control Treated
## All       429.       185
## weightit   32.07     185
## ow_bw      31.62     185
## ow        108.64     185

Looking at the mean differences (in the columns Diff.weightit, Diff.ow_bw, and Diff.ow in the first stable), we can see that the GBM weights from WeightIt alone did not balance the covariate means, whereas both set of SBW weights from optweight did. However, in the second table, we can see big differences in the KS statistics between the SBW weights that incorporated the base weights and those that didn’t. The KS statistics for the SBW weights that incorporated the base weights (listed in the KS.ow_bw column) are very close to those for the GBM weights (listed in the KS.weightit column) because the estimated weights are very close to the GBM weights. In contrast, the SBW weights that didn’t incorporate the base weights have very high KS statistics for some covariates (listed in the KS.ow column); they are unable to take advantage of the distribution-balancing properties of the original GBM weights.

In this way, incorporating the base weights provides a middle ground between the GBM weights and the basic SBW weights: they ensure exact balance on the means while attempting to retain as much similarity to the GBM weights as possible, thereby inheriting some of their balancing properties. Unfortunately, one of those properties is also a very low ESS, though in this case, little ESS is lost by enforcing the additional balance constraints. Using different norms with base weights can also be more effective than using with them uniform base weights, as different norms prioritize similarity to the base weights in ways that may retain different properties².

Dual variables

Dual variables, also known as “shadow prices”, are part of the output of the optimization problem that represent how “active” a given constraint is at the optimum (Zubizarreta 2015). A large dual variable means that relaxing the constraint will allow the objective function to reach a lower value. They are related to the coefficients on covariates in a propensity score model, representing how much each covariate is contributing to the estimation of the weights. Zubizarreta (2015) describes the utility of dual variables after SBW: they can be used to determine which covariates can have constraints relaxed to improve precision and which covariates can have constraints tightened without affecting precision. The dual variables are available in optweight() output in the duals component, but they can also be plotted using plot(). They can also be useful for diagnosing convergence failure; often, a constraint that is impossible to meet will have a high dual variable when no solution can be found.

Below, we’ll demonstrate how we can use the dual variables to see how to modify constraints to try to take advantage of the bias-variance trade-off. First we’ll estimate SBW weights with tolerances of .02 for all covariates.

tols <- process_tols(treat ~ age + educ + race + married + nodegree +
                       re74 + re75, data = lalonde,
                     tols = .02)

ow <- optweight(treat ~ age + educ + race + married + nodegree +
                  re74 + re75, data = lalonde,
                estimand = "ATT",
                tols = tols)

summary(ow, weight.range = FALSE)

##                   Summary of weights
## 
## 
## - Weight statistics:
## 
##            L2    L1    L∞ Rel Ent # Zeros
## treated 0.    0.    0.      0.          0
## control 1.616 1.267 4.212   1.118       0
## 
## - Effective Sample Sizes:
## 
##            Control Treated
## Unweighted   429.      185
## Weighted     118.8     185

We can print the dual variables in the duals component of the output object and plot them with plot():

ow$duals

##   constraint      cov    dual
## 1     target      age 0.24485
## 2     target     educ 0.62674
## 3     target     race 5.66548
## 4     target  married 1.05266
## 5     target nodegree 1.61135
## 6     target     re74 0.71501
## 7     target     re75 0.04373

plot(ow)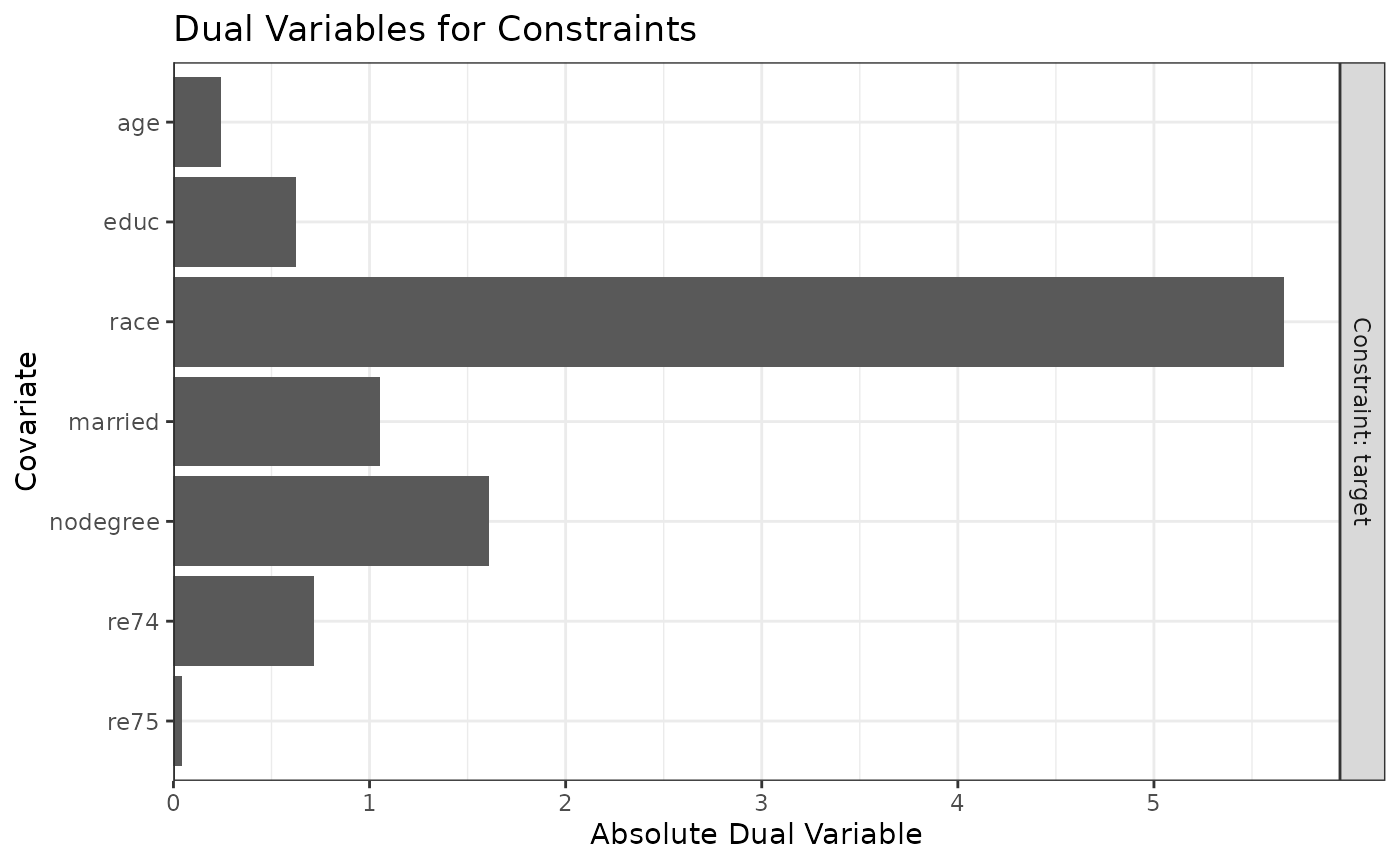

From this, it’s clear that race has the largest dual variable, and re75 has the smallest. That means we can likely get the biggest gains in ESS by relaxing the constraint for race, whereas tightening the constraint for re75 will have little effect on the ESS. Below, we relax the balance constraint for race to .1.

tols["race"] <- .1

ow2 <- optweight(treat ~ age + educ + race + married + nodegree +
                   re74 + re75, data = lalonde,
                 estimand = "ATT",
                 tols = tols)

summary(ow2, weight.range = FALSE)

##                   Summary of weights
## 
## 
## - Weight statistics:
## 
##            L2    L1    L∞ Rel Ent # Zeros
## treated 0.    0.    0.       0.         0
## control 1.424 1.113 3.638    0.91       0
## 
## - Effective Sample Sizes:
## 
##            Control Treated
## Unweighted   429.      185
## Weighted     141.7     185

By relaxing the constraint on race, our ESS increased by quite a bit. We would not see the same increase had we instead relaxed the constraint on a covariate with a smaller dual variable, like re75. Below, we restore all balance constraints to .02 and then set the balance constraint for re75 to .1.

tols[] <- .02
tols["re75"] <- .1

ow3 <- optweight(treat ~ age + educ + race + married + nodegree +
                   re74 + re75, data = lalonde,
                 estimand = "ATT",
                 tols = tols)

summary(ow3, weight.range = FALSE)

##                   Summary of weights
## 
## 
## - Weight statistics:
## 
##            L2    L1    L∞ Rel Ent # Zeros
## treated 0.    0.    0.      0.          0
## control 1.616 1.267 4.207   1.118       0
## 
## - Effective Sample Sizes:
## 
##            Control Treated
## Unweighted   429.      185
## Weighted     118.8     185

This had virtually no effect on the ESS (relative to all balance tolerances being equal to .02). However, this also suggests we can tighten the constraint on re75 without much loss in ESS. Below, we decrease the tolerance on re75 to 0:

tols["re75"] <- 0

ow4 <- optweight(treat ~ age + educ + race + married + nodegree +
                   re74 + re75, data = lalonde,
                 estimand = "ATT",
                 tols = tols)

summary(ow4, weight.range = FALSE)

##                   Summary of weights
## 
## 
## - Weight statistics:
## 
##            L2    L1    L∞ Rel Ent # Zeros
## treated 0.    0.    0.       0.         0
## control 1.617 1.269 4.229    1.12       0
## 
## - Effective Sample Sizes:
## 
##            Control Treated
## Unweighted   429.      185
## Weighted     118.7     185

We see that despite the tighter tolerance, the ESS remains about the same. For reference, below are the balance statistics and ESSs for all four sets of weights:

cobalt::bal.tab(treat ~ age + educ + race + married + nodegree +
                  re74 + re75, data = lalonde,
                weights = list(ow  = ow$weights,
                               ow2 = ow2$weights,
                               ow3 = ow3$weights,
                               ow4 = ow4$weights))

## Balance Measures
##                Type Diff.ow Diff.ow2 Diff.ow3 Diff.ow4
## age         Contin.    0.02     0.02    0.020     0.02
## educ        Contin.    0.02     0.02    0.020     0.02
## race_black   Binary    0.02     0.10    0.020     0.02
## race_hispan  Binary    0.00     0.00    0.000     0.00
## race_white   Binary   -0.02    -0.10   -0.020    -0.02
## married      Binary   -0.02    -0.02   -0.020    -0.02
## nodegree     Binary    0.02     0.02    0.020     0.02
## re74        Contin.   -0.02    -0.02   -0.020    -0.02
## re75        Contin.    0.02     0.02    0.026    -0.00
## 
## Effective sample sizes
##     Control Treated
## All   429.      185
## ow    118.8     185
## ow2   141.7     185
## ow3   118.8     185
## ow4   118.7     185

Again we can see that relaxing the balance constraint for race increases the ESS significantly, whereas either tightening or relaxing the constraint for re75 has little effect on the ESS.

Multivariate treatments

It is possible to supply balance constraints for multiple (i.e., multivariate) treatments simultaneously to estimate a single set of weights that satisfies them all. This approach is described by Chen and Zhou (2023) in the context of multiple continuous treatments. optweightMV() provides an interface to balancing multiple treatments and works similarly to optweight(), though with the ability to supply multiple balancing formulas. Though this can be used with conceptually distinct treatments, it can also sometimes be useful to use it with multiple transformations of a single treatment; for example, Greifer (2020) found that in order to eliminate the bias due to certain kinds of imbalance with a continuous treatment, the square of the centered treatment must be uncorrelated with the covariates, in addition to the treatment itself being uncorrelated with the covariates.

To use optweightMV(), supply a list of balancing formulas to the formula.list argument. The tols.list argument must also be a list with a vector of tolerances for each treatment, each with a value for each covariate. However, targets should be a vector with a value for each unique covariate since one cannot specify multiple targets for the same covariate. Below is example (not run) of how to specify a call to optweightMV():

owmv <- optweightMV(list(t1 ~ x1 + x2 + x3,
                         t2 ~ x1 + x2 + x3,
                         t3 ~ x1 + x2 + x3),
                    data = data,
                    tols.list = list(c(x1 = .01, x2 = .01, x3 = .01),
                                     c(x1 = .02, x2 = .02, x3 = .02),
                                     c(x1 = .03, x2 = .03, x3 = .03)),
                    targets = c(x1 = 10, x2 = .34, x3 = 5.5))

The syntax can be abbreviated by supplying a single value in each element of tols.list that is applied to all covariates, e.g., tols.list = list(.01, .02, .03); or, if the same vector of balance tolerance is desired for all covariates for all treatments, a list with a single vector, e.g., tols.list = list(c(x1 = .01, x2 = .01, x3 = .01)); or, if the same tolerance is desired for all covariates and all treatments, a list with a single value, e.g., tols.list = list(.02). targets can be omitted to target the ATE (i.e., to balance the covariates at their means in the sample), but no other estimands can be specified.

One might be tempted to use optweightMV() to estimate balancing weights for longitudinal treatments. While this is possible, it’s not as simple as supplying a balancing formula for each treatment balancing the treatment and covariate history to that treatment (Yiu and Su 2020). Zhou and Wodtke (2020) describe how to specify balance constraints for entropy balancing with longitudinal treatments, and they involve balancing not the covariate directly but rather the residuals in regressions of the covariates on treatment and covariate histories. Functionality for this specific method is not present in optweight, but is available in the rbw package. It may be possible to implement this in optweight manually, but I cannot advise on how to do so.

`optweight.svy()`

When the goal is not to balance treatment groups to each other or to some target population but rather to balance one sample to a target distribution, one can use optweight.svy() instead of optweight(). The .svy suffix is an indication that can be used as a method to generate survey weights so that the sample generalizes to a population of interest with specific means. optweight.svy() works just like optweight() except that no treatment variable is specified and targets should be specified.

This is useful in the context of matching-adjusted indirect comparison [MAIC; Signorovitch et al. (2010)], which involves weighting a given trial sample to resemble the covariate distribution of some other trial’s sample. MAIC as originally described is equivalent to entropy balancing (Phillippo et al. 2020), which can be requested by setting norm = "entropy".

Below, we demonstrate weighting the control subset of lalonde to resemble a specific target population. As with optweightit(), it can be helpful to use process_targets() to simplify specification of the covariates means. If all variables in the dataset are to be specified, the formula can be omitted (for both process_targets() and optweight.svy()).

lalonde_c <- subset(lalonde, treat == 0,
                    select = -c(treat))

targets <- process_targets(lalonde_c)

targets

##  - targets:
##         age        educ  race_black race_hispan  race_white     married    nodegree        re74 
##     28.0303     10.2354      0.2028      0.1422      0.6550      0.5128      0.5967   5619.2365 
##        re75        re78 
##   2466.4844   6984.1697

To request individual means, the targets can be set to those values. To allow a covariate mean to vary freely, one can either omit it from the calls to process_targets() and optweight.svy() or set the target value to NA. We’ll do that for re78, and set specific targets for the other variables except re75, which we’ll leave at its mean.

targets["age"] <- 40
targets["educ"] <- 9
targets[c("race_black", "race_hispan", "race_white")] <- c(.2, .2, .6)
targets["married"] <- .6
targets["nodegree"] <- .6
targets["re74"] <- 1000
is.na(targets["re78"]) <- TRUE

targets

##  - targets:
##         age        educ  race_black race_hispan  race_white     married    nodegree        re74 
##        40.0         9.0         0.2         0.2         0.6         0.6         0.6      1000.0 
##        re75        re78 
##      2466.5          NA

We can supply these to optweight.svy(). This time we’ll set min.w to 0 to allow those with weights of 0 to be effectively dropped from the sample.

ow_s <- optweight.svy(lalonde_c,
                      targets = targets,
                      min.w = 0)

ow_s

## An optweight.svy object
##  - number of obs.: 429
##  - norm minimized: "l2"
##  - sampling weights: present
##  - base weights: present
##  - covariates: age, educ, race, married, nodegree, re74, re75, re78

summary(ow_s)

##                   Summary of weights
## 
## - Weight ranges:
## 
##     Min                                 Max
## all   0 |---------------------------| 13.54
## 
## - Units with the 5 most extreme weights:
##                                      
##        404   152    111     19     16
##  all 9.488 9.669 11.326 11.429 13.537
## 
## 
## - Weight statistics:
## 
##        L2  L1    L∞ # Zeros
## all 2.237 1.5 12.54     307
## 
## - Effective Sample Sizes:
## 
##             Total
## Unweighted 429.  
## Weighted    71.44

We can see that the weights required to move the sample toward our specified target decrease the ESS by quite a bit, and several units were given weights of 0. This can actually be a good thing if it means less data needs to be collected since those with weights of 0 are not necessary for subsequent analysis. We can examine the weighted covariate means using cobalt::col_w_means() as before, with the estimated weights supplied to s.weights:

cobalt::col_w_mean(lalonde_c, s.weights = ow_s$weights)

##         age        educ  race_black race_hispan  race_white     married    nodegree        re74 
##        40.0         9.0         0.2         0.2         0.6         0.6         0.6      1000.0 
##        re75        re78 
##      2466.5      4725.6

We can see that the weighted mean of re78 is whatever minimized the L2 norm of the weights since no constraint was placed on it. As with optweight(), we can see how much each constraint contributed to the increase in variability by examining the dual variables:

plot(ow_s)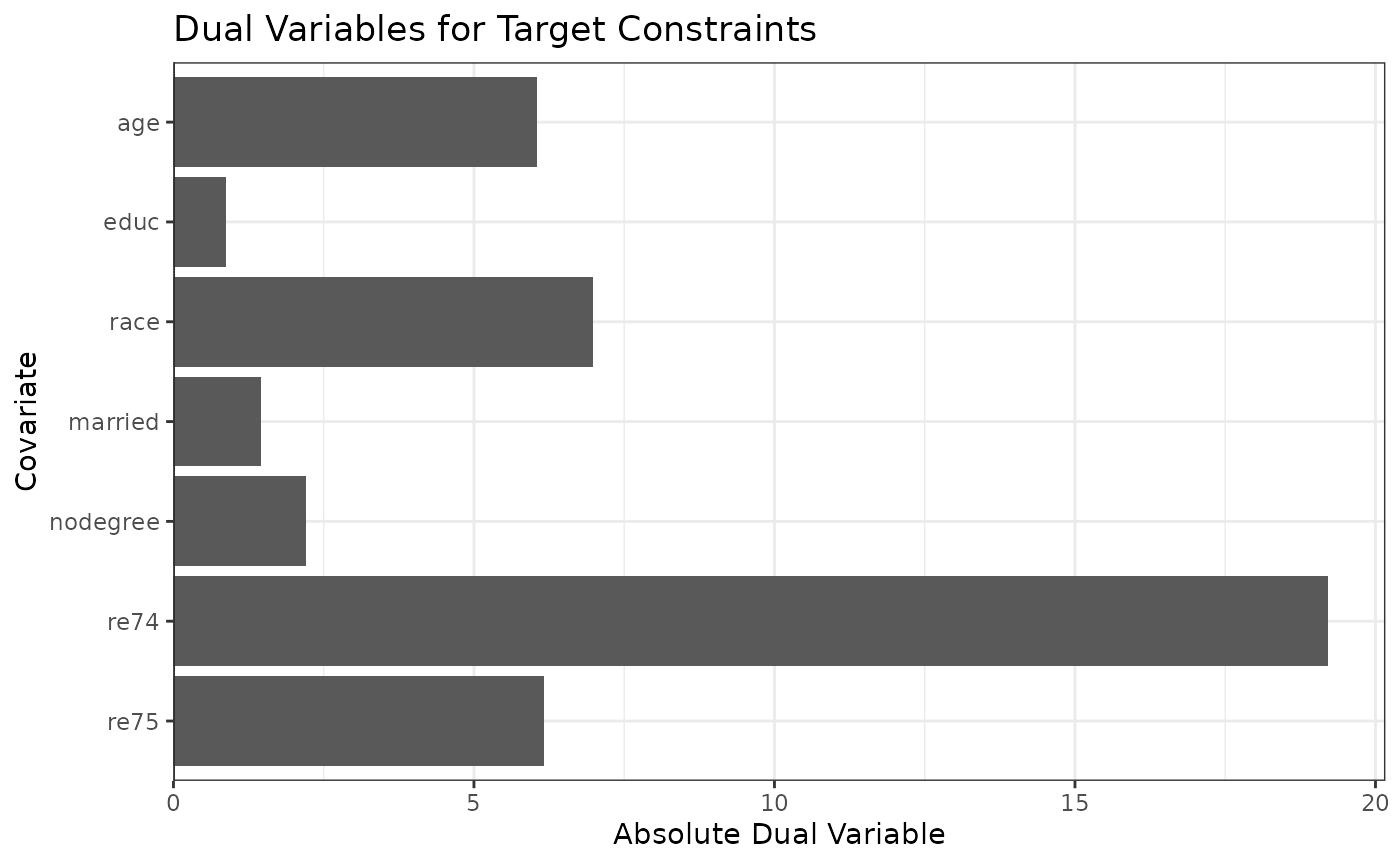

Here it’s clear that the constraint on re74 is contributing the most, and that relaxing the constraint would have the greatest impact on ESS. The constraint can be relaxed either by changing the target to one closer to that of the original data (or closer to where it would be if no constraint was placed on re74) or by setting a more relaxed tolerance for re74 using tols. We’ll use the latter option below:

tols <- process_tols(lalonde_c, tols = 0)

tols["re74"] <- 300

tols

##  - tols:
##      age     educ     race  married nodegree     re74     re75     re78 
##        0        0        0        0        0      300        0        0

Here we set the tolerance for re74 to be 300. We need to set std.cont = FALSE to tell optweight.svy() that the tolerance for continuous variables should be in raw units, not standardized units. Now we can interpret our constraint as allowing the weighted mean for re74 to be within 300 of its specified target of 1000.

ow_s2 <- optweight.svy(lalonde_c,
                       targets = targets,
                       min.w = 0,
                       tols = tols,
                       std.cont = FALSE)

summary(ow_s2, weight.range = FALSE)

##                   Summary of weights
## 
## 
## - Weight statistics:
## 
##       L2   L1    L∞ # Zeros
## all 2.07 1.44 10.68     290
## 
## - Effective Sample Sizes:
## 
##             Total
## Unweighted 429.  
## Weighted    81.15

This increased the ESS of the weights, and below we can see that the weighted mean for re74 is at most 300 away from 1000, while the other variables are at their specified targets.

cobalt::col_w_mean(lalonde_c, s.weights = ow_s2$weights)

##         age        educ  race_black race_hispan  race_white     married    nodegree        re74 
##        40.0         9.0         0.2         0.2         0.6         0.6         0.6      1300.0 
##        re75        re78 
##      2466.5      4710.8

Estimating effects

Because SBW weights function just like IPW weights, the same procedures can be used to estimate the effect of treatment in an SBW-weighted sample. One only needs to run a regression of the outcome on the treatment with the weights incorporated. It is critical that the usual standard errors from lm() or glm(), etc., are not used; special standard errors are required after weighting. See vignette("estimating-effects", package = "WeightIt") for more details on estimating effects after weighting. WeightIt provides tools for facilitating this when weights are estimated using WeightIt::weightit(), which provides an interface to optweight(), though with slightly fewer options available.

Often, the best way to account for uncertainty in estimating a treatment effect after SBW is by bootstrapping. This ensures variability due to estimating the weights is correctly incorporated. The fractional weighted bootstrap (Xu et al. 2020) is often particularly effective because no units are dropped from the sample in each bootstrap replication. When bootstrapping cannot be used (e.g., because it is too computationally demanding or the specified constraints cannot be expected to be satisfied in all bootstrap samples), using a robust standard error can be an acceptable alternative.

Below, we demonstrate both approaches with the lalonde data. First, we estimate the weights for the ATT and fit the outcome model.

ow <- optweight(treat ~ age + educ + race + married + nodegree +
                  re74 + re75, data = lalonde,
                estimand = "ATT",
                eps = 1e-5)

fit <- lm(re78 ~ treat, data = lalonde,
          weights = ow$weights)

coef(fit)

## (Intercept)       treat 
##        5145        1204

Again, we must not use the usual standard errors produced by running summary() on the lm() output; we must use either bootstrapping or a robust standard error. First, we’ll use bootstrapping with fwb, which implements the fractional weighted bootstrap. This involves drawing a set of weights from a distribution and performing the entire analysis with these weights incorporated. These weights should be supplied to the s.weights argument in optweight() and multiplied by the returned weights before being used in lm()³. We can use update() to re-estimate the SBW weights and weighted regression model in each bootstrap replication.

library(fwb)

bootfun <- function(data, w) {
  ow_boot <- update(ow, s.weights = w)
  fit_boot <- update(fit, weights = ow_boot$weights * w)
  
  coef(fit_boot)
}

set.seed(123)

boot <- fwb(lalonde, bootfun,
            R = 250, # more is always better, but slower
            verbose = FALSE)

summary(boot, ci.type = "wald", p.value = TRUE)

##             Estimate Std. Error CI 2.5 % CI 97.5 % z value Pr(>|z|)    
## (Intercept)     5145        570     4028      6261    9.03   <2e-16 ***
## treat           1204        772     -310      2718    1.56     0.12    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

To use a robust standard error, it’s easiest to use functions in the marginaleffects package. Supply the output of lm() to marginaleffects::avg_comparisons() with vcov = "HC3" to request a robust standard error for the treatment effect estimate.

library(marginaleffects)

avg_comparisons(fit,
                variables = "treat",
                vcov = "HC3",
                newdata = subset(treat == 1))

## 
##  Estimate Std. Error    z Pr(>|z|)   S 2.5 % 97.5 %
##      1204        824 1.46    0.144 2.8  -411   2819
## 
## Term: treat
## Type: response
## Comparison: 1 - 0

Robust standard errors treat the weights as fixed, which often yields larger standard errors than the bootstrap.

References

Angeles Resa, María de los, and José R. Zubizarreta. 2020. “Direct and Stable Weight Adjustment in Non-Experimental Studies With Multivalued Treatments: Analysis of the Effect of an Earthquake on Post-Traumatic Stress.” Journal of the Royal Statistical Society Series A: Statistics in Society 183 (4): 1387–1410. https://doi.org/10.1111/rssa.12561.

Chan, Kwun Chuen Gary, Sheung Chi Phillip Yam, and Zheng Zhang. 2016. “Globally Efficient Non-Parametric Inference of Average Treatment Effects by Empirical Balancing Calibration Weighting.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 78 (3): 673–700. https://doi.org/10.1111/rssb.12129.

Chattopadhyay, Ambarish, Eric R. Cohn, and José R. Zubizarreta. 2024. “One-Step Weighting to Generalize and Transport Treatment Effect Estimates to a Target Population.” The American Statistician 78 (3): 280–89. https://doi.org/10.1080/00031305.2023.2267598.

Chattopadhyay, Ambarish, Noah Greifer, and José R. Zubizarreta. 2024. “Lmw: Linear Model Weights for Causal Inference.” Observational Studies 10 (2): 33–62. https://doi.org/10.1353/obs.2024.a946582.

Chattopadhyay, Ambarish, Christopher H. Hase, and José R. Zubizarreta. 2020. “Balancing Vs Modeling Approaches to Weighting in Practice.” Statistics in Medicine 39 (24): 3227–54. https://doi.org/10.1002/sim.8659.

Chattopadhyay, Ambarish, and José R Zubizarreta. 2023. “On the Implied Weights of Linear Regression for Causal Inference.” Biometrika 110 (3): 615–29. https://doi.org/10.1093/biomet/asac058.

Chattopadhyay, Ambarish, and José R. Zubizarreta. 2024. “Causation, Comparison, and Regression.” Harvard Data Science Review 6 (1). https://doi.org/10.1162/99608f92.87c6125f.

Chen, Juan, and Yingchun Zhou. 2023. “Causal Effect Estimation for Multivariate Continuous Treatments.” Biometrical Journal 65 (5): 2200122. https://doi.org/10.1002/bimj.202200122.

Cohn, Eric R., and José R. Zubizarreta. 2025. “Weighting for Causal Inference in Mental Health Research.” International Journal of Methods in Psychiatric Research 34 (2): e70018. https://doi.org/10.1002/mpr.70018.

Dorie, Vincent, Jennifer Hill, Uri Shalit, Marc Scott, and Dan Cervone. 2019. “Automated Versus Do-It-Yourself Methods for Causal Inference: Lessons Learned from a Data Analysis Competition.” Statistical Science 34 (1): 43–68. https://doi.org/10.1214/18-STS667.

Fong, Christian, Chad Hazlett, and Kosuke Imai. 2018. “Covariate Balancing Propensity Score for a Continuous Treatment: Application to the Efficacy of Political Advertisements.” The Annals of Applied Statistics 12 (1): 156–77. https://doi.org/10.1214/17-AOAS1101.

Greifer, Noah. 2020. “Estimating Balancing Weights for Continuous Treatments Using Constrained Optimization.” PhD thesis. https://doi.org/10.17615/DYSS-B342.

Hainmueller, J. 2012. “Entropy Balancing for Causal Effects: A Multivariate Reweighting Method to Produce Balanced Samples in Observational Studies.” Political Analysis 20 (1): 25–46. https://doi.org/10.1093/pan/mpr025.

Jackson, Dan, Kirsty Rhodes, and Mario Ouwens. 2021. “Alternative Weighting Schemes When Performing Matching-Adjusted Indirect Comparisons.” Research Synthesis Methods 12 (3): 333–46. https://doi.org/10.1002/jrsm.1466.

Jiang, Ziren, Joseph C. Cappelleri, Margaret Gamalo, Yong Chen, Neal Thomas, and Haitao Chu. 2024. “A Comprehensive Review and Shiny Application on the Matching-Adjusted Indirect Comparison.” Research Synthesis Methods 15 (4): 671–86. https://doi.org/10.1002/jrsm.1709.

Källberg, David, and Ingeborg Waernbaum. 2023. “Large Sample Properties of Entropy Balancing Estimators of Average Causal Effects.” Econometrics and Statistics, November. https://doi.org/10.1016/j.ecosta.2023.11.004.

Phillippo, David M., Sofia Dias, A. E. Ades, and Nicky J. Welton. 2020. “Equivalence of Entropy Balancing and the Method of Moments for Matching-Adjusted Indirect Comparison.” Research Synthesis Methods 11 (4): 568–72. https://doi.org/10.1002/jrsm.1416.

Signorovitch, James E., Eric Q. Wu, Andrew P. Yu, Charles M. Gerrits, Evan Kantor, Yanjun Bao, Shiraz R. Gupta, and Parvez M. Mulani. 2010. “Comparative Effectiveness Without Head-to-Head Trials: A Method for Matching-Adjusted Indirect Comparisons Applied to Psoriasis Treatment with Adalimumab or Etanercept.” PharmacoEconomics 28 (10): 935–45. https://doi.org/10.2165/11538370-000000000-00000.

Tübbicke, Stefan. 2022. “Entropy Balancing for Continuous Treatments.” Journal of Econometric Methods 11 (1): 71–89. https://doi.org/10.1515/jem-2021-0002.

Vegetabile, Brian G., Beth Ann Griffin, Donna L. Coffman, Matthew Cefalu, Michael W. Robbins, and Daniel F. McCaffrey. 2021. “Nonparametric Estimation of Population Average Dose-Response Curves Using Entropy Balancing Weights for Continuous Exposures.” Health Services and Outcomes Research Methodology 21 (1): 69–110. https://doi.org/10.1007/s10742-020-00236-2.

Wang, Jixian. n.d. “On Matching-Adjusted Indirect Comparison and Calibration Estimation.” https://doi.org/10.48550/arXiv.2107.11687.

Wang, Yixin, and Jose R. Zubizarreta. 2020. “Minimal Dispersion Approximately Balancing Weights: Asymptotic Properties and Practical Considerations.” Biometrika 107 (1): 93–105. https://doi.org/10.1093/biomet/asz050.

Xu, Li, Chris Gotwalt, Yili Hong, Caleb B. King, and William Q. Meeker. 2020. “Applications of the Fractional-Random-Weight Bootstrap.” The American Statistician 74 (4): 345–58. https://doi.org/10.1080/00031305.2020.1731599.

Yiu, Sean, and Li Su. 2020. “Joint Calibrated Estimation of Inverse Probability of Treatment and Censoring Weights for Marginal Structural Models.” Biometrics n/a (n/a). https://doi.org/https://doi.org/10.1111/biom.13411.

Zhao, Qingyuan, and Daniel Percival. 2017. “Entropy Balancing Is Doubly Robust.” Journal of Causal Inference 5 (1). https://doi.org/10.1515/jci-2016-0010.

Zhou, Xiang, and Geoffrey T. Wodtke. 2020. “Residual Balancing: A Method of Constructing Weights for Marginal Structural Models.” Political Analysis 28 (4): 487–506. https://doi.org/10.1017/pan.2020.2.

Zubizarreta, José R. 2015. “Stable Weights That Balance Covariates for Estimation with Incomplete Outcome Data.” Journal of the American Statistical Association 110 (511): 910–22. https://doi.org/10.1080/01621459.2015.1023805.

Noah Greifer

2025-09-18

Introduction

Using optweight

`tols`

`norm`

`estimand` and `targets`

Sampling weights and base weights

Dual variables

Multivariate treatments

`optweight.svy()`

Estimating effects

Further reading

References

Using optweight to Estimate Stable Balancing Weights

Noah Greifer

2025-09-18

Introduction

Using optweight

tols

norm

estimand and targets

Sampling weights and base weights

Dual variables

Multivariate treatments

optweight.svy()

Estimating effects

Further reading

References

`tols`

`norm`

`estimand` and `targets`

`optweight.svy()`