Plots the dual variables resulting from optweight(), optweightMV(), or optweight.svy() in a way similar to
figure 2 of Zubizarreta (2015), which explains how to interpret these
values.
Arguments
- x
an
optweight,optweightMV, oroptweight.svyobject; the output of a call tooptweight(),optweightMV(), oroptweight.svy().- ...
ignored.
- which.treat
for
optweightMVobjects, an integer corresponding to which treatment to display. Only one may be displayed at a time.
Details
Dual variables represent the cost of changing the constraint on the objective function minimized to estimate the weights. For covariates with large values of the dual variable, tightening the constraint will increase the variability of the weights, and relaxing the constraint will decrease the variability of the weights, both to a greater extent than would doing the same for covariate with small values of the dual variable. See optweight() and vignette("optweight") for more information on interpreting dual variables.
References
Zubizarreta, J. R. (2015). Stable Weights that Balance Covariates for Estimation With Incomplete Outcome Data. Journal of the American Statistical Association, 110(511), 910–922. doi:10.1080/01621459.2015.1023805
See also
optweight(), optweightMV(), or optweight.svy() to estimate the weights and the dual variables.
plot.summary.optweight() for plots of the distribution of weights.
Examples
library("cobalt")
data("lalonde", package = "cobalt")
tols <- process_tols(treat ~ age + educ + married +
nodegree + re74, data = lalonde,
tols = .1)
#Balancing covariates between treatment groups (binary)
ow1 <- optweight(treat ~ age + educ + married +
nodegree + re74, data = lalonde,
tols = tols,
estimand = "ATT")
summary(ow1) # Note the L2 divergence and effective
#> Summary of weights
#>
#> - Weight ranges:
#>
#> Min Max
#> treated 1 || 1.
#> control 0 |---------------------------| 1.595
#>
#> - Units with the 5 most extreme weights by group:
#>
#> 1 2 3 4 5
#> treated 1 1 1 1 1
#> 79 118 127 156 164
#> control 1.595 1.595 1.595 1.595 1.595
#>
#>
#> - Weight statistics:
#>
#> L2 L1 L∞ Rel Ent # Zeros
#> treated 0. 0. 0 0. 0
#> control 0.532 0.462 1 0.181 0
#>
#> - Effective Sample Sizes:
#>
#> Control Treated
#> Unweighted 429. 185
#> Weighted 334.41 185
# sample size (ESS)
plot(ow1) # age has a low value, married is high
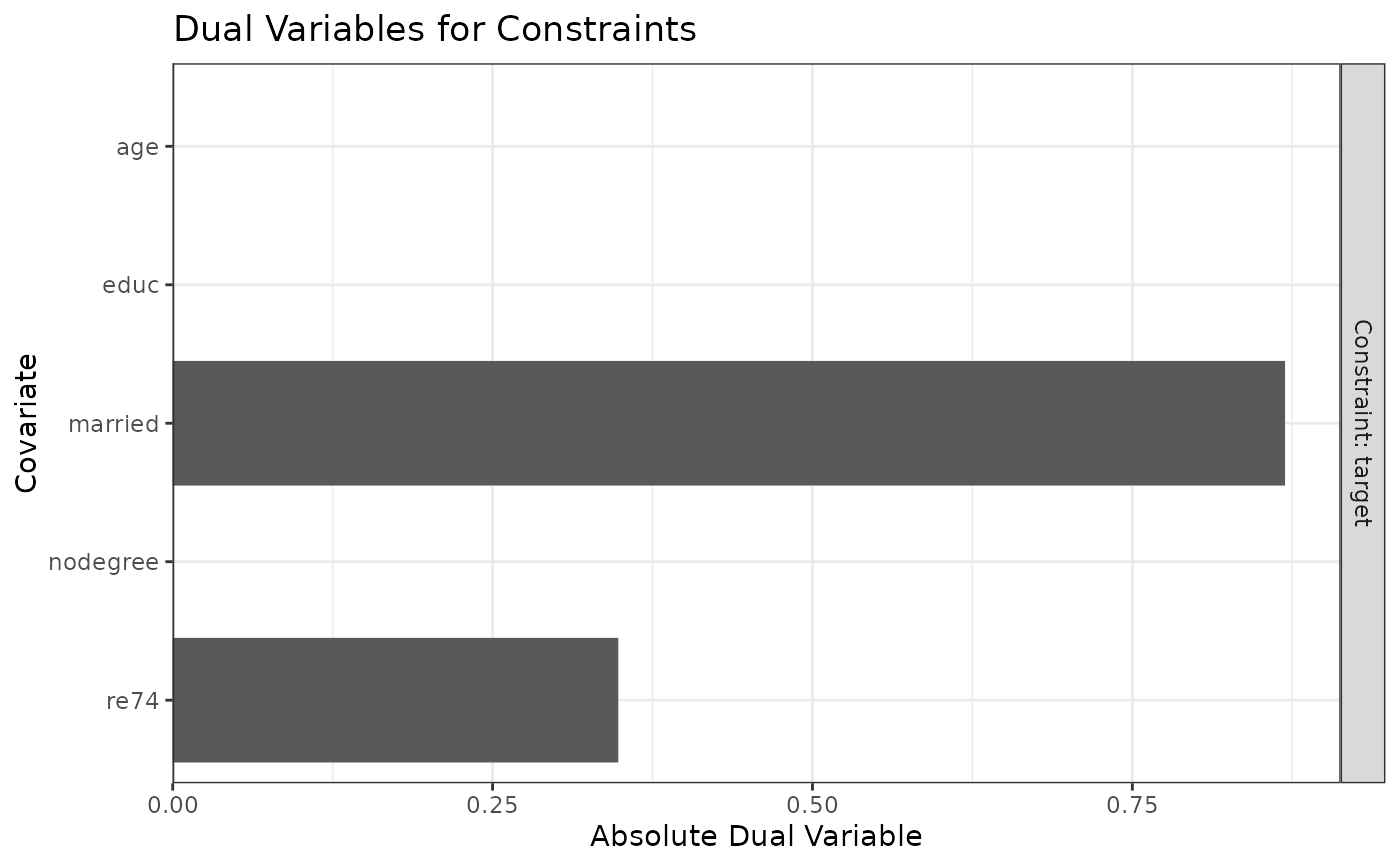tols["age"] <- 0
ow2 <- optweight(treat ~ age + educ + married +
nodegree + re74, data = lalonde,
tols = tols,
estimand = "ATT")
summary(ow2) # Notice that tightening the constraint
#> Summary of weights
#>
#> - Weight ranges:
#>
#> Min Max
#> treated 1 || 1.
#> control 0 |---------------------------| 1.754
#>
#> - Units with the 5 most extreme weights by group:
#>
#> 1 2 3 4 5
#> treated 1 1 1 1 1
#> 419 404 412 387 395
#> control 1.734 1.744 1.744 1.754 1.754
#>
#>
#> - Weight statistics:
#>
#> L2 L1 L∞ Rel Ent # Zeros
#> treated 0. 0. 0 0. 0
#> control 0.534 0.465 1 0.183 0
#>
#> - Effective Sample Sizes:
#>
#> Control Treated
#> Unweighted 429. 185
#> Weighted 333.86 185
# on age had a negligible effect on the
# variability of the weights and ESS
tols["age"] <- .1
tols["married"] <- 0
ow3 <- optweight(treat ~ age + educ + married +
nodegree + re74, data = lalonde,
tols = tols,
estimand = "ATT")
summary(ow3) # In contrast, tightening the constraint
#> Summary of weights
#>
#> - Weight ranges:
#>
#> Min Max
#> treated 1 || 1.
#> control 0 |---------------------------| 1.871
#>
#> - Units with the 5 most extreme weights by group:
#>
#> 1 2 3 4 5
#> treated 1 1 1 1 1
#> 419 404 412 387 395
#> control 1.857 1.864 1.864 1.871 1.871
#>
#>
#> - Weight statistics:
#>
#> L2 L1 L∞ Rel Ent # Zeros
#> treated 0. 0. 0 0. 0
#> control 0.676 0.647 1 0.277 0
#>
#> - Effective Sample Sizes:
#>
#> Control Treated
#> Unweighted 429. 185
#> Weighted 294.35 185
# on married had a large effect on the
# variability of the weights, shrinking
# the ESS