Subgroup Analysis After Propensity Score Matching Using R

Packages You’ll Need

We’ll need a few R packages for this analysis. We’ll need {MatchIt} and {optmatch} for the matching, {cobalt} for the balance assessment, {marginaleffects} for estimating the treatment effects, and {sandwich} for computing the standard errors. You can install those using the code below:

install.packages(c("MatchIt", "optmatch", "cobalt",
                   "marginaleffects", "sandwich"))

Let’s get into it!

Step 1: Subgroup Matching

Our first step is to perform the matching. Although there are a few strategies for performing matching for subgroup analysis, in general subgroup-specific matching tends to work best, though it requires a little extra work.

We’ll do this by splitting the dataset by race and performing a separate matching analysis within each one.

#Splitting the data
lalonde_b <- subset(lalonde, race == "black")
lalonde_h <- subset(lalonde, race == "hispan")
lalonde_w <- subset(lalonde, race == "white")

Here we’ll use full matching because 1:1 matching without replacement, the most common (but worst) way to do propensity score matching, doesn’t work well in this dataset. The process described below works exactly the same for 1:1 and most other kinds of matching as it does for full matching. We’ll estimate propensity scores in each subgroup, here using probit regression, which happens to yield better balance than logistic regression does.

library("MatchIt")

#Matching in race == "black"
m.out_b <- matchit(treat ~ age + educ + married + nodegree + re74 + re75,
                   data = lalonde_b, method = "full", estimand = "ATT",
                   link = "probit")

#Matching in race == "hispan"
m.out_h <- matchit(treat ~ age + educ + married + nodegree + re74 + re75,
                   data = lalonde_h, method = "full", estimand = "ATT",
                   link = "probit")

#Matching in race == "black"
m.out_w <- matchit(treat ~ age + educ + married + nodegree + re74 + re75,
                   data = lalonde_w, method = "full", estimand = "ATT",
                   link = "probit")

Step 2: Assessing Balance within Subgroups

We need to assess subgroup balance; we can do that using summary() on each matchit object, or we can use functions from {cobalt}.

Below are examples of using summary() and cobalt::bal.tab() on one matchit object at a time¹:

summary(m.out_b)

## 
## Call:
## matchit(formula = treat ~ age + educ + married + nodegree + re74 + 
##     re75, data = lalonde_b, method = "full", link = "probit", 
##     estimand = "ATT")
## 
## Summary of Balance for All Data:
##          Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max
## distance        0.6587        0.6121          0.4851     0.7278    0.1134   0.1972
## age            25.9808       26.0690         -0.0121     0.4511    0.0902   0.2378
## educ           10.3141       10.0920          0.1079     0.5436    0.0336   0.0807
## married         0.1859        0.2874         -0.2608          .    0.1015   0.1015
## nodegree        0.7244        0.6437          0.1806          .    0.0807   0.0807
## re74         2155.0132     3117.0584         -0.1881     0.9436    0.0890   0.2863
## re75         1490.7221     1834.4220         -0.1043     1.0667    0.0480   0.1441
## 
## Summary of Balance for Matched Data:
##          Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max Std. Pair Dist.
## distance        0.6587        0.6577          0.0096     1.0403    0.0095   0.0705          0.0374
## age            25.9808       27.6538         -0.2292     0.3644    0.1148   0.2073          1.3764
## educ           10.3141       10.1368          0.0861     0.6552    0.0228   0.0684          1.0485
## married         0.1859        0.1822          0.0096          .    0.0037   0.0037          0.6236
## nodegree        0.7244        0.7286         -0.0096          .    0.0043   0.0043          0.7548
## re74         2155.0132     2998.6538         -0.1650     0.7590    0.0513   0.2025          0.7256
## re75         1490.7221     2120.7862         -0.1911     0.8819    0.0798   0.1912          0.8430
## 
## Sample Sizes:
##               Control Treated
## All             87.       156
## Matched (ESS)   36.04     156
## Matched         87.       156
## Unmatched        0.         0
## Discarded        0.         0

library("cobalt")
bal.tab(m.out_b, un = TRUE, stats = c("m", "ks"))

## Balance Measures
##              Type Diff.Un  KS.Un Diff.Adj KS.Adj
## distance Distance  0.4851 0.1972   0.0096 0.0705
## age       Contin. -0.0121 0.2378  -0.2292 0.2073
## educ      Contin.  0.1079 0.0807   0.0861 0.0684
## married    Binary -0.1015 0.1015   0.0037 0.0037
## nodegree   Binary  0.0807 0.0807  -0.0043 0.0043
## re74      Contin. -0.1881 0.2863  -0.1650 0.2025
## re75      Contin. -0.1043 0.1441  -0.1911 0.1912
## 
## Sample sizes
##                      Control Treated
## All                    87.       156
## Matched (ESS)          36.04     156
## Matched (Unweighted)   87.       156

We can also get a clearer sense of balance overall using bal.tab() by directly supplying the matching weights.

#Initialize the weights
fm_weights <- numeric(nrow(lalonde))

#Assign the weights based on the subgroup
fm_weights[lalonde$race == "black"] <- m.out_b$weights
fm_weights[lalonde$race == "hispan"] <- m.out_h$weights
fm_weights[lalonde$race == "white"] <- m.out_w$weights

bal.tab(treat ~ age + educ + married + nodegree + re74 + re75,
        data = lalonde, weights = fm_weights, cluster = "race",
        stats = c("m", "ks"), abs = TRUE, cluster.summary = TRUE)

## Balance by cluster
## 
##  - - - Cluster: black - - - 
## Balance Measures
##             Type Diff.Adj KS.Adj
## age      Contin.   0.2292 0.2073
## educ     Contin.   0.0861 0.0684
## married   Binary   0.0037 0.0037
## nodegree  Binary   0.0043 0.0043
## re74     Contin.   0.1650 0.2025
## re75     Contin.   0.1911 0.1912
## 
## Effective sample sizes
##                0   1
## Unadjusted 87.   156
## Adjusted   36.04 156
## 
##  - - - Cluster: hispan - - - 
## Balance Measures
##             Type Diff.Adj KS.Adj
## age      Contin.   0.2298 0.1848
## educ     Contin.   0.2888 0.2762
## married   Binary   0.0604 0.0604
## nodegree  Binary   0.1024 0.1024
## re74     Contin.   0.1323 0.3188
## re75     Contin.   0.1220 0.2351
## 
## Effective sample sizes
##                0  1
## Unadjusted 61.   11
## Adjusted   26.24 11
## 
##  - - - Cluster: white - - - 
## Balance Measures
##             Type Diff.Adj KS.Adj
## age      Contin.   0.4137 0.2126
## educ     Contin.   0.4246 0.1840
## married   Binary   0.0025 0.0025
## nodegree  Binary   0.1653 0.1653
## re74     Contin.   0.2846 0.4165
## re75     Contin.   0.0825 0.1444
## 
## Effective sample sizes
##                 0  1
## Unadjusted 281.   18
## Adjusted    49.49 18
##  - - - - - - - - - - - - - - 
## 
## Balance summary across all clusters
##             Type Mean.Diff.Adj Max.Diff.Adj Mean.KS.Adj Max.KS.Adj
## age      Contin.        0.2909       0.4137      0.2016     0.2126
## educ     Contin.        0.2665       0.4246      0.1762     0.2762
## married   Binary        0.0222       0.0604      0.0222     0.0604
## nodegree  Binary        0.0907       0.1653      0.0907     0.1653
## re74     Contin.        0.1940       0.2846      0.3126     0.4165
## re75     Contin.        0.1319       0.1911      0.1902     0.2351
## 
## Total effective sample sizes across clusters
##                 0   1
## Unadjusted 429.   185
## Adjusted   111.77 185

Using the cluster argument produces balance tables in each subgroup and, because we specified cluster.summary = TRUE, a balance table summarizing across subgroups. To suppress display of the subgroup-specific balance tables (which may be useful if you have many subgroups), you can specify which.cluster = .none.

To make a plot displaying the balance statistics visually, we can use cobalt::love.plot():

love.plot(treat ~ age + educ + married + nodegree + re74 + re75,
        data = lalonde, weights = fm_weights, cluster = "race",
        stats = c("m", "ks"), abs = TRUE,
        which.cluster = .none, agg.fun = "max")

## Warning: Standardized mean differences and raw mean differences are present in the same plot. 
## Use the 'stars' argument to distinguish between them and appropriately label the x-axis.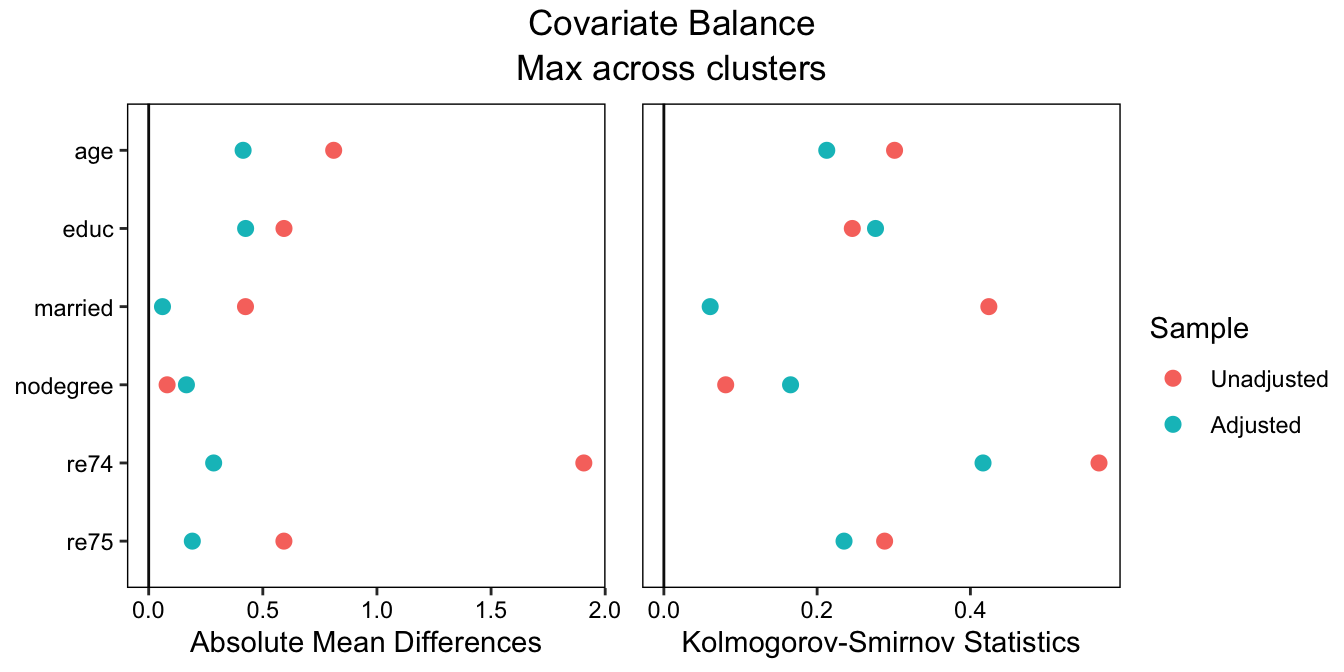

See the {cobalt} vignette on customizing love.plot() to see how to finely control the appearance of the plot.

From this output, we can see that balance is actually pretty bad; the greatest standardized mean difference (SMD) across subgroups after matching is around .46, which is way too big. In a realistic scenario, we would try different matching methods, maybe resorting to weighting, until we found good balance across the subgroups. In order to validly interpret the subgroup-specific effects and tests for moderation, we need to achieve balance in each subgroup, not just overall. We didn’t get good balance here, but to stay focused on the rest of the procedure, we’ll move forward as if we did.

Step 3: Fitting the Outcome Model

Next, we’ll fit the outcome model. It’s important to remember that the outcome model is an intermediate step for estimating the treatment effect; no quantity estimated by the model needs to correspond to the treatment effect directly. We’ll be using a marginal effects procedure to estimate the treatment effects in the next section.

First, we’ll extract the matched datasets from the matchit objects. We can’t just use the matching weights we extracted earlier because we also need subclass (i.e., pair) membership. We’ll use match.data() from {MatchIt} to extract the matched datasets, which contain the matching weights and subclass membership in the weights and subclass columns, respectively, and use rbind() to bind them into a single combined dataset².

#Extract the matched datasets
matched_data_b <- match.data(m.out_b)
matched_data_h <- match.data(m.out_h)
matched_data_w <- match.data(m.out_w)

#Combine them using rbind()
matched_data <- rbind(matched_data_b,
                      matched_data_h,
                      matched_data_w)

names(matched_data)

##  [1] "treat"    "age"      "educ"     "race"     "married"  "nodegree" "re74"     "re75"     "re78"     "re78_0"   "distance" "weights"  "subclass"

Next, we can fit the outcome model. The choice of which model to fit should depend primarily on the best model for the outcome; because we have a binary outcome, we’ll use logistic regression.

It’s usually a good idea to include covariates in the outcome model. It’s also usually a good idea to allow the treatment to interact with the covariates in the outcome model. It’s also usually a good idea to fit separate models within each subgroup. Combining this all yields a pretty complicated model, which is why it will be so important to use a marginal effects procedure rather than trying to interpret the model’s coefficients. Here’s how we fit this model:

fit <- glm(re78_0 ~ race * (treat * (age + educ + married + nodegree +
                                       re74 + re75)),
           data = matched_data, weights = weights,
           family = "quasibinomial")

We’re not even going to look at the output of this model, which has 42 parameters. If the model doesn’t fit with your dataset, you can remove interactions between the treatment and some covariates or remove the covariates altogether.

For a linear model, you can use lm() and remove the family argument. We used family = "quasibinomial" because we want logistic regression for our binary outcome but we are using the matching weights, which otherwise create a (harmless but annoying) warning when run with family = "binomial".

Step 4: Estimate the Treatment Effects

Finally, we can estimate the treatment effects. To do so, we’ll use an average marginal effects procedure as implemented in {marginaleffects}³. First, we’ll estimate the average marginal effect overall, averaging across the subgroups. Again, we’re hoping for a negative treatment effect, which indicates the risk of having zero income decreased among those who received the treatment. Because we are estimating the ATT, we need to subset the data for which the average marginal effects are computed to just the treated units, which we do using the newdata argument (which can be omitted when the ATE is the target estimand). We also need to supply pair membership to ensure the standard errors are correctly computed, which we do by supplying the subclass variable containing pair membership to the vcov argument. In general, we need to supply the weights to the wts argument of avg_comparisons() as well (though, in this case, because we are estimating the ATT and all weights are 1 for the treated group, it doesn’t make a difference).

library("marginaleffects")

#Estimate the overall ATT
avg_comparisons(fit, variables = "treat",
                newdata = subset(matched_data, treat == 1),
                vcov = ~subclass, wts = "weights")

## 
##   Term Contrast Estimate Std. Error      z Pr(>|z|)  2.5 % 97.5 %
##  treat    1 - 0  0.03434    0.04405 0.7795  0.43566 -0.052 0.1207
## 
## Prediction type:  response 
## Columns: type, term, contrast, estimate, std.error, statistic, p.value, conf.low, conf.high

The estimated risk difference is 0.02305 with a high p-value and a confidence interval containing 0, indicating no evidence of an effect overall. (Note: this doesn’t mean there is no effect! The data are compatible with effects anywhere within the confidence interval, which includes negative and positive effects of a moderate size!)

New, let’s estimate the subgroup-specific effects by supplying the subgrouping variable, "race", to the by argument:

avg_comparisons(fit, variables = "treat",
                newdata = subset(matched_data, treat == 1),
                vcov = ~subclass, wts = "weights",
                by = "race")

## 
##   Term          Contrast   race Estimate Std. Error      z  Pr(>|z|)    2.5 %   97.5 %
##  treat mean(1) - mean(0)  black  0.06985    0.05168  1.352 0.1764930 -0.03144  0.17114
##  treat mean(1) - mean(0) hispan -0.18744    0.07293 -2.570 0.0101667 -0.33038 -0.04450
##  treat mean(1) - mean(0)  white -0.13790    0.04886 -2.822 0.0047678 -0.23367 -0.04214
## 
## Prediction type:  response 
## Columns: type, term, contrast, race, estimate, std.error, statistic, p.value, conf.low, conf.high, predicted, predicted_hi, predicted_lo

Here, we see that actually there is evidence of treatment effects within subgroups! In the subgroups hispan and white, we see moderately sized negative effects with small p-values and confidence intervals excluding 0, suggesting that there treatment effects in these subgroups.

We can also test whether the treatment effects differ between groups using the hypothesis argument of avg_comparisons():

avg_comparisons(fit, variables = "treat",
                newdata = subset(matched_data, treat == 1),
                vcov = ~subclass, wts = "weights",
                by = "race", hypothesis = "pairwise")

## 
##                                                                Term Estimate Std. Error       z  Pr(>|z|)    2.5 % 97.5 %
##  (black,treat,mean(1) - mean(0)) - (hispan,treat,mean(1) - mean(0))  0.25729    0.08939  2.8785 0.0039961  0.08210 0.4325
##   (black,treat,mean(1) - mean(0)) - (white,treat,mean(1) - mean(0))  0.20775    0.07112  2.9211 0.0034877  0.06836 0.3471
##  (hispan,treat,mean(1) - mean(0)) - (white,treat,mean(1) - mean(0)) -0.04954    0.08779 -0.5643 0.5725398 -0.22160 0.1225
## 
## Prediction type:  response 
## Columns: type, term, estimate, std.error, statistic, p.value, conf.low, conf.high

We can see evidence that the treatment effect differs between the black and hispan groups, and between the black and white groups. With many subgroups, it might be useful to adjust your p-values for multiple comparisons, which we can do using p.adjust(), e.g.,

p.adjust(comp$p.value, method = "holm")

if comp contained the avg_comparisons() output above.

Congratulations! You’ve done a subgroup analysis!

Step 5: Reporting Your Results

A fair bit needs to be included when reporting your results to ensure your analysis is replicable and can be correctly interpreted by your audience. The key things to report are the following:

• The method of estimating the propensity score and performing the matching (noting that these were done within subgroups), including the estimand targeted and whether that estimand was respected by the procedure (using, e.g., a caliper changes the estimand from the one you specify). This should also include the packages used and, even better, the functions used. If you’re using {MatchIt}, the documentation should also tell you which papers to cite.
• A quick summary of other methods you might have tried and why you went with the one you went with (i.e., because it yielded better balance, a greater effective sample size, etc.).
• Covariate balance, measured broadly; this can include a balance table, a balance plot (like one produced by cobalt::love.plot()), or a summary of balance (like providing the largest SMD and KS statistic observed across subgroups). Make sure your description of balance reflects the subgroups, e.g., by having separate tables or plots for each subgroup or clarifying that the statistics presented are averages or the worst case across subgroups.
• The outcome model you used, especially specifying the form of the model used and how/whether covariates entered the model. Also mention the method used to compute the standard errors (e.g., cluster-robust standard errors with pair membership as the clustering variable).
• Details of the marginal effects procedure used, including the package used, and the method to compute the standard errors (in this case, the delta method, which is the only method available in {marginaleffects}).
• The treatment effect estimates along with their p-values and confidence intervals, both overall and within subgroups.