Contrast an effect curve with a reference point

reference_curve() creates a new effect curve as the contrast between each point on a given effect curve and a specified point along that curve. The new curve is called a "reference effect curve".

Usage

reference_curve(x, reference)

Arguments

x

an effect_curve object; the output of a call to adrf() or a function that modifies it.

reference

numeric; the value of the treatment to use as the reference value.

Value

An object of class reference_curve, which inherits from effect_curve, with the value supplied to reference as an additional attribute.

Details

The value supplied to reference is added as a grid point on the reference effect curve using the interpolation method described in effect_curve. The delta method is used to compute the variance of the difference between each point along the effect curve and the reference point.

See also

• adrf() for computing the ADRF

• plot.effect_curve() for plotting the reference effect curve

• summary.effect_curve() for testing hypotheses about the reference effect curve

• summary.curve_est() for performing inference on individual points on an effect curve, including a reference effect curve

• point_contrast() for effect curve estimates to each other (rather than to a single point)

Examples

data("nhanes3lead")

fit <- lm(Math ~ poly(logBLL, 5) *
            (Male + Age + Race + PIR +
               Enough_Food),
          data = nhanes3lead)

# ADRF of logBLL on Math, unconditional
# inference
adrf1 <- adrf(fit, treat = "logBLL")

# Differences between ADRF estimates and estimate
# at `logBLL = 0`
ref1 <- reference_curve(adrf1, reference = 0)

ref1
#> An <effect_curve> object
#> 
#>  - curve type: ADRF reference
#>  - response: Math
#>  - treatment: logBLL
#>    + range: -0.3567 to 2.4248
#>  - reference level: 0
#>  - inference: unconditional
#> 

# Plot the reference effect curve
plot(ref1)


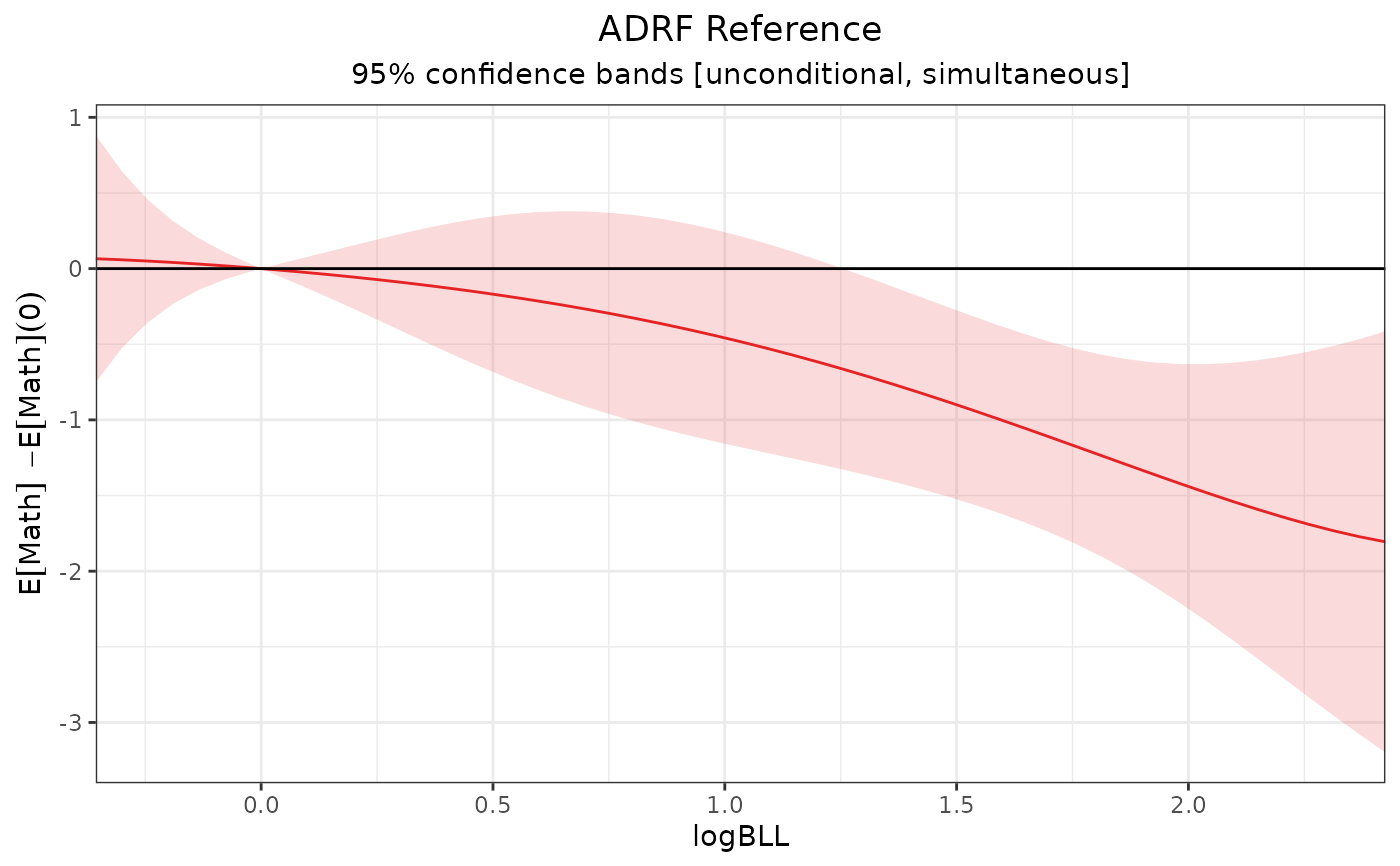# Reference effect curve estimates at given points
ref1(logBLL = c(0, 1, 2)) |>
  summary()
#>                  ADRF Reference Estimates
#> ───────────────────────────────────────────────────────────
#>  logBLL Estimate Std. Error      t  P-value  CI Low CI High
#>       0   0.0000     0.0000      .        .  0.0000  0.0000
#>       1  -0.4579     0.2662 -1.720   0.1461 -1.0437  0.1279
#>       2  -1.4403     0.3074 -4.685 < 0.0001 -2.1170 -0.7637
#> ───────────────────────────────────────────────────────────
#> Inference: unconditional, simultaneous
#> Confidence level: 95% (t* = 2.201, df = 2473)
#> Reference: logBLL = 0 | Null value: 0

# Test if reference effect curve is 0 (equivalent
# to testing if ADRF is flat)
summary(ref1)
#>                   Omnibus Curve Test
#> ───────────────────────────────────────────────────────
#> H₀: ADRF difference from reference (logBLL = 0) is 0
#>     for values of logBLL between -0.3567 and 2.4248
#> 
#>   P-value
#>  < 0.0001
#> ───────────────────────────────────────────────────────
#> Computed using the Imhof approximation